라플라스 연산자
라플라스 또는 라플라시안 연산자는 2차 미분 연산자의 일종으로, 기울기의 발산이다.
이전 포스팅에서 소벨 연산자에 대해 다룬적이 있다. 엣지 부근에서 픽셀의 값이 뛰는 것을 확인할 수 있었다.
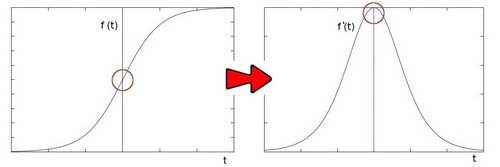
만약에 여기에 2차 미분을 취하면 어떻게 될까?
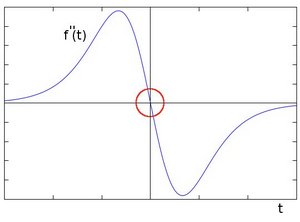
2차미분은 말 그대로 1차 미분값을 다시 한번 미분하는 방법을 말하는데, 2차미분의 장점은 엣지의 중심부분을 찾을 수 있다는 점이다. 2차 미분한 그래프를 보면 엣지부분이 0으로 부호가 바뀌게 되는 것을 확인할 수 있다. 이를 변곡점 또는 영교차(zero crossing)라고 한다. 이 기준을 사용하여 이미지의 엣지를 검출할 수 있다. 이 때, 라플라시안 연산을 사용할 수 있다.
라플라시안 방정식은 다음과 같다.
OpenCV에서 제공하는 라플라시안 함수는 다음과 같다.
Imgproc.Laplacian(Mat src, Mat dst, int ddepth, int ksize)
src : 입력 영상 dst : 결과 영상 ddepth : 출력영상 데이터 타입, -1이면 입력 영상과 같은 데이터 타입 사용.
라플라시안 함수는 미분의 차수가 필요하지 않다는 점을 제외하고는 소벨 함수와 동일한 파라미터를 취한다. 커널에 대한 ksize는 소벨 미분의 커널과 정확하게 같으며, 사실상 그 픽셀이 2차 미분의 계산을 위해 샘플링하는 영역의 크기를 정한다. 실제로 라플라시안 에서 이미지의 기울기를 사용하기 때문에 내부적으로는 소벨 함수를 호출하여 계산을 수행한다.
레나 이미지를 Grayscale로 변경하고 라플라시안 필터를 적용한 결과는 다음과 같다.
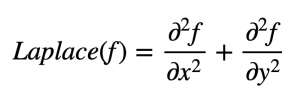



0개의 댓글