이진화 임계값 결정
지난 포스팅에서 임계값을 통해 이미지를 이진화 하는 방법에 대해서 알아보았다.
이진화 된 이미지를 얻을 때 가장 중요한 점은 바로 임계값을 어떻게 또는 무엇으로 결정하냐는 것이다. 임계값을 조금씩 변경하면서 사람의 눈으로 확인하여 가장 좋은 결과값을 얻는 것도 하나의 방법이지만 이러한 반복적인 작업 없이도 자동으로 적절한 임계값을 한번에 찾을 수 있는 방법을 오츠 노부유키(Otsu Nobuyuki)라는 사람이 고안했다.
오츠의 알고리즘(Otsu’s method)
오츠가 고안한 방법(Otsu’s method)은 다음을 가정할 때 가장 우수한 결과를 보인다.
- 원본 이미지가 배경과 객체 두개로 구성되어 있을 때
- 원본 이미지의 히스토그램 분포가 두개의 봉우리(Bimodal)형태를 가질 때
- 두 봉우리 사이의 골이 깊고 날카로울 때
오츠의 방법은 이미지의 히스토그램을 사용하여 각 클래스(흑,백 또는 0,255)의 분산을 최소화하는 방법을 사용한다. 일반적으로 이런 방법은 Bimodal 이미지에서 가장 효과적인 값을 구할 수 있다. 이러한 이미지의 히스토그램에서는 명확하게 표현되는 두개의 봉우리가 있는데 이는 각각 다른 값의 범위를 표현하게 된다.
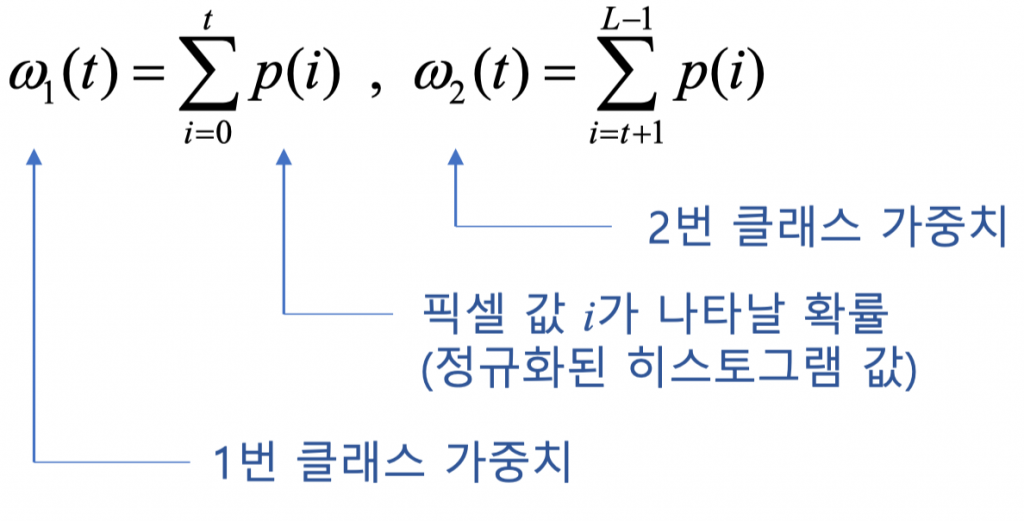
이 핵심 아이디어는 히스토그램에서 가중치 분산을 최소화한 결과로 주어진 임계값 t를 사용하여 두 클래스(흑 or 백)로 분리한다. 이를 수식으로 나타내면 다음과 같다
핵심은 within-class variance가 최소가 되는 t(0~255)값을 찾는 것이다. 이때 1,2번 클래스의 분산을 계산하는 과정은 반복적인 작업이라 시간이 오래걸리게 된다.
그래서 오츠 논문을 보면 다음과 같은 Between-class variance라는 개념을 새로 정의하게 된다.
전체 분산에서 within-class 분산을 빼는 것인데. 결국 이 개념은 within-class 분산을 최소화하면 between-class 분산이 최대화 된다는 것을 기초로 한다.
전체 분산은 사실 한번만 계산하면 되는 상수이지만, 결국 수식을 전개하면 평균을 계산하는 수식이 계속 나오기 때문에 계산하는데 시간이 오래걸리기는 마찬가지다.
그래서 평균값을 계산할 때 다음과 같이 이전 평균값을 그대로 이용한다.
점화식(Recursion)을 이용하기 때문에 효율적인 계산으로 계산속도가 빨라지게 된다.
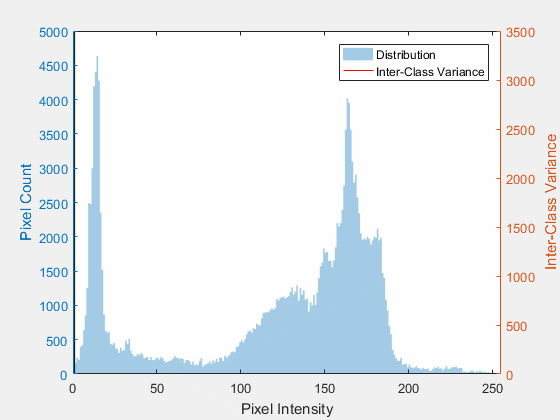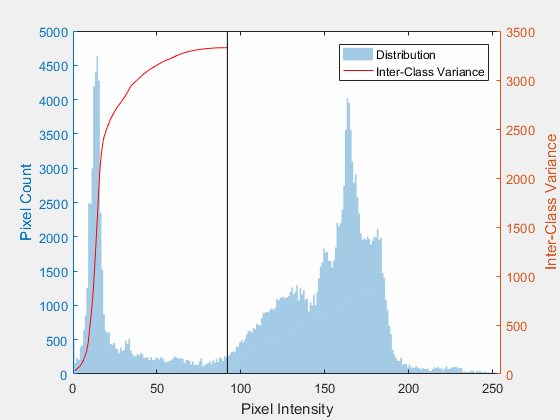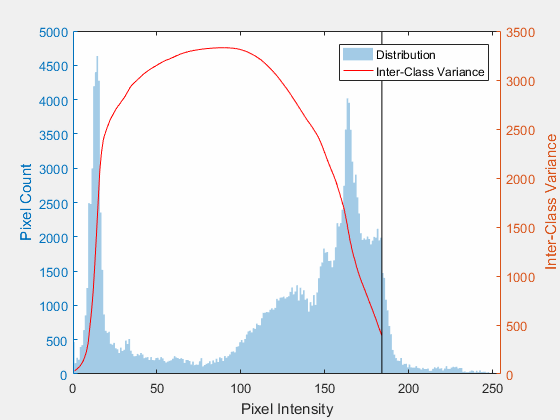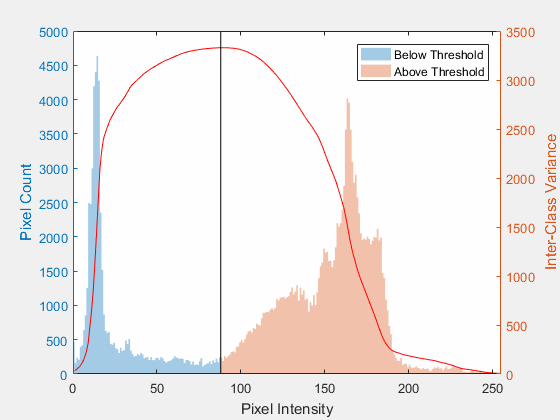
오츠 알고리즘을 가시화 한 다음 GIF 이미지를 확인하자.
입력영상의 히스토그램에 대해서 T값을 0부터 255까지 증가시키면서 between class variance값(빨간곡선)이 어떤 형태로 분포되는지 보는 것이다. 위 그래프에서는 대략 T값이 85~90정도가 될 때 between class variance가 최대가 되는 것을 확인할 수 있다. 이 값으로 이진화를 할 때 이진화가 가장 잘 된다라고 볼 수 있다.
OpenCV에서 Otsu 알고리즘을 사용하는 것은 간단하다. 기존에 threshold 함수를 사용할 때 THRESH_OTSU 플래그를 추가하면 된다.
안드로이드에서 구현한 예제를 살펴보자.
// grayscale로 변환
val graySrc = Mat()
Imgproc.cvtColor(src, graySrc, Imgproc.COLOR_BGR2GRAY)
// otsu 이진화 적용
val dst = Mat()
val threshold = Imgproc.threshold(
graySrc, dst,
0.0, 255.0, // 픽셀값의 분포 범위 0~255
Imgproc.THRESH_BINARY or Imgproc.THRESH_OTSU // THRESH_OTSU 플래그 함께 사용
)
// 회색 -> 컬러 변경
Imgproc.cvtColor(dst, dst, Imgproc.COLOR_GRAY2BGR)
// 계산된 Threshold 출력
Imgproc.putText(dst, "Threshold = $threshold", ...)
// 이미지 출력
...
레나, 세포 이미지, 쌀알 이미지 총 3가지 준비하여 위 코드를 통해 가장 적절한 T값을 찾고 출력 했다.
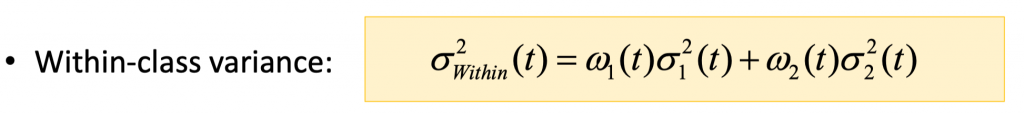
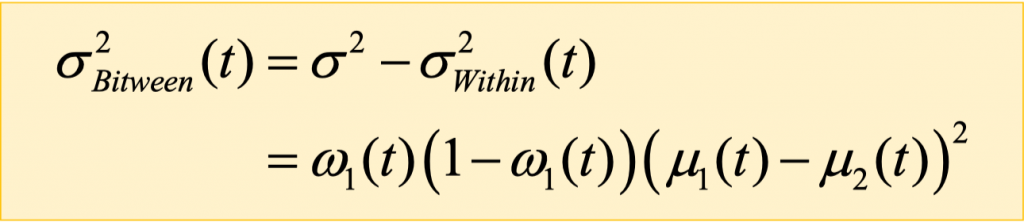
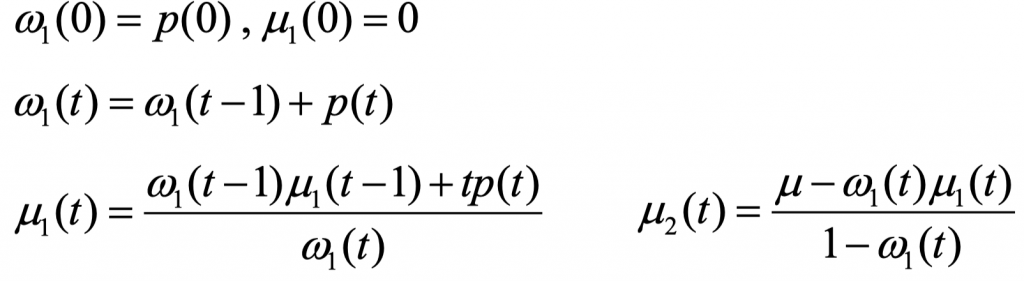

0개의 댓글