Moments
모멘트(moments)는 한 점이나 축에 대한 분포를 나타낸다. 그렇기 때문에 OpenCV에서 모멘트는 이미지 픽셀 강도의 평균을 나타낸다. 즉, 모멘트란 영상의 형태를 표현하는 일련의 실수값이라고 볼 수 있다.
컴퓨터는 카메라 영상과 같은 실시간 이미지 처리시에 이미지의 픽셀 값들을 어떤 숫자로 변환한다. 영상에서 두개의 연속된 프레임(이미지) 사이에는 반드시 어떠한 변화 또는 움직임이 있기 마련이다. 모멘트를 통해 연속 된 이미지 사이에서의 움직임을 발견할 수 있다. 모멘트는 이미지의 객체가 회전, 이동 또는 기타 다른 형태의 변형을 겪을 때 변경되지 않은 상태로 남아 있는 이미지의 특징을 감지하는 데 사용된다. 다시 한번 이야기 하지만 이미지 모멘트는 픽셀 강도 분포를 측정하는 파라미터다.
모멘트 구하기
이미지에서 모멘트를 구하는 공식은 다음과 같다.
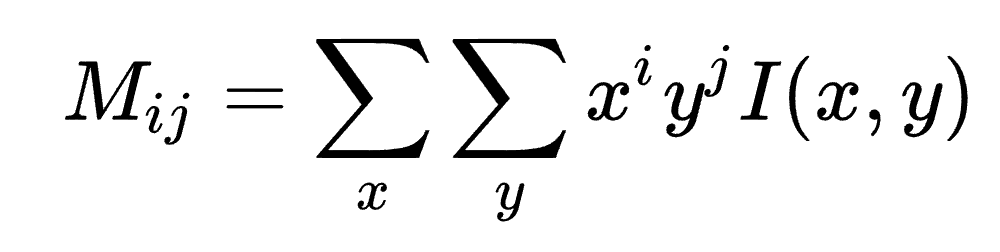
모멘트 Mij는 차수(i,j)에 대해 계산되며, I(x,y)는 이미지의 각 픽셀에 대한 강도가 된다. 이 공식을 통해 0차 모멘트 , 1차 모멘트, 2차 모멘트와 같은 여러 모멘트를 계산할 수 있다.
모멘트를 계산하는 예제를 살펴보자. 이해를 돕기 위해 단순히 이진 픽셀 값이 포함된 아래의 이미지를 사용하여 모멘트를 구해보자.

여기에서는 0차 모멘트를 구해보도록 하자. 즉 i = 0, j = 0 이다. M00을 구하는 풀이는 다음과 같다.
I(1,1) + I(1,2) + I(1,3) + I(1,4) = 0 + 1 + 1 + 0 = 2 For x = 2: I(2,1) + I(2,2) + I(2,3) + I(2,4) = 0 + 1 + 1 + 0 = 2 For x = 3: I(3,1) + I(3,2) + I(3,3) + I(3,4) = 0 + 1 + 1 + 0 = 2 For x = 4: I(4,1) + I(4,2) + I(4,3) + I(4,4) = 0 + 0 + 0 + 0 = 0
위 풀이로 얻은 합을 구하면 M00 = 6 이라는 사실을 알 수 있다.
이와 유사한 방식으로 1차 모멘트(M10 및 M01) 및 2차 모멘트(M11)를 구할 수 있다.
중심 모멘트(Central moments)
위 모멘트 공식의 문제는 모멘트가 x와 y위치에 민감하다는 점이다. 우리는 모멘트 형태가 형태가 있는 위치에 독립적이길 원한다. 그렇기 때문에 중심 모멘트(centeral moments)를 사용할 수 있다.
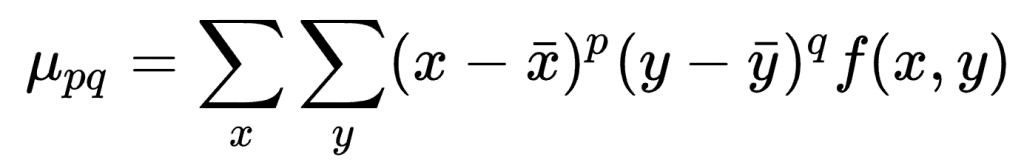
기본적인 공식은 동일하나, 유일한 차이점은 x와 y를 취하는 대신 x에서 x의 평균을 빼고, 마찬가지로 y에서 y의 평균을 뺀다는 점이다. 여기서 p와 q는 모멘트의 차수다. 3차까지 중식 모멘트를 구하면 다음과 같다.
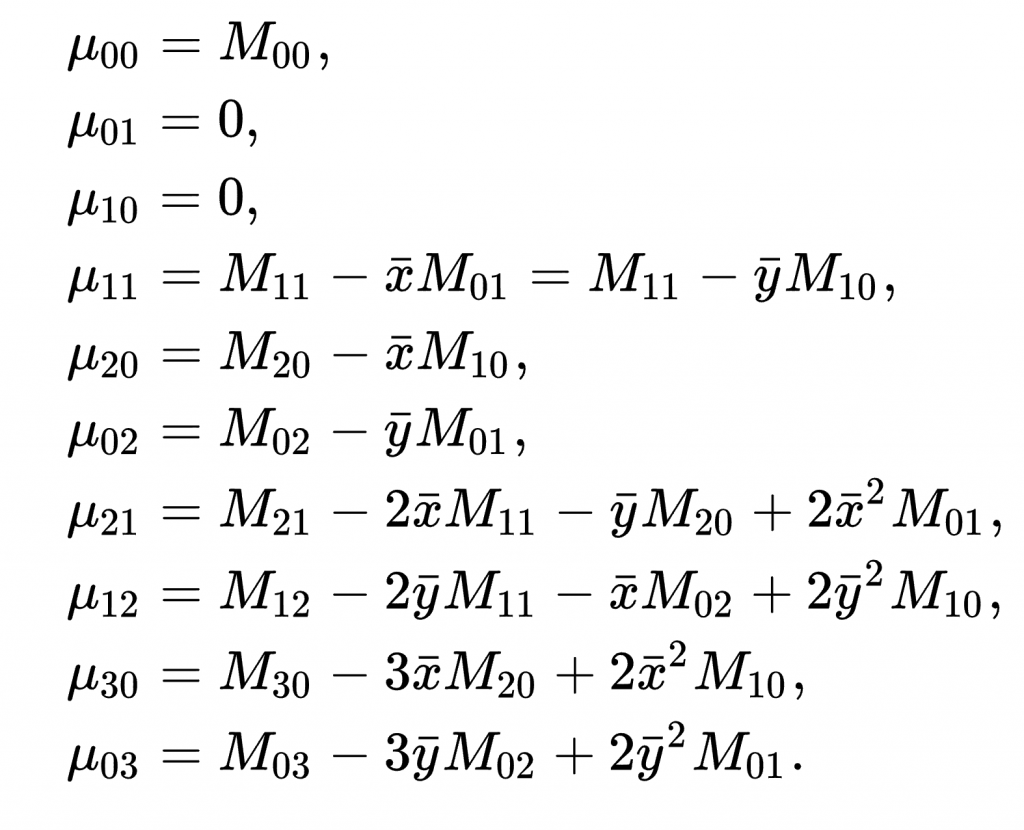
물론 μ00 = M00 이고, μ10 과 μ01의 중심 모멘트는 모두 0이라는 것은 바로 알 수 있다. 따라서 고차 모멘트는 비중심 모멘트와 같지만 전체 객체의 중심 좌표에서 측정된다. 이러한 측정값은 중심과 관련되기 때문에 객체가 이미지의 임의의 위치에 나타나더라도 변경되지 않는다. 이를 ‘이동에 불변'(translational invariant)하다라고 한다.
OpenCV Moments 객체에는 mu00이나 mu10, mu01이 없다는 사실을 알 수 있다. 이것은 위에서 언급한 것처럼 항상 mu00 = m00 및 mu01 = mu10 = 0으로 간단하기 때문이다. 이러한 이유로 중복된 정보를 저장하는 것은 메모리를 낭비하므로 이를 구조체에 포함하지 않는다.
정규화된 중심 모멘트
중심 모멘트를 통해 두 이미지 상의 객체가 같은지 비교할 수 있다. 하지만 동일한 객체를 포함하는 두 이미지를 생성하는 과정에서 많은 환경적인 요인이 작용하므로 컴퓨터상으로 계산할 때는 동일한 객체로 인식하지 못할 수도 있다. 예를 들어 카메라로 사진을 찍을 때 물체가 렌즈에서 얼마나 멀리 떨어져 있느냐에 따라 객체의 크기가 달라진다.
중심 모멘트가 평균을 제거함으로써 이동에 불변하다는 상수를 얻는 것처럼 정규화 된 중심 모멘트는 물체의 전체크기를 나눠 스케일에 불변한 특징을 갖는다. 정규화 된 중심 모멘트의 공식은 다음과 같다.
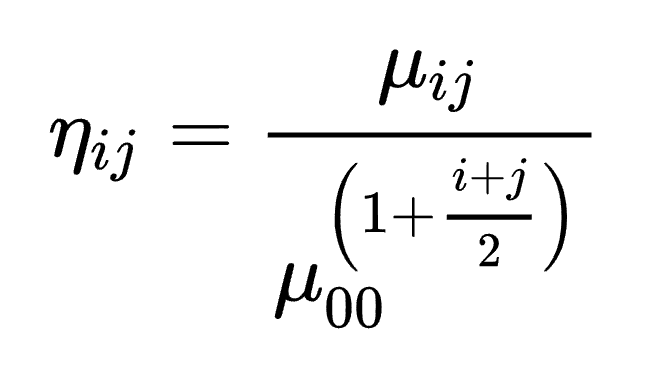
이 공식에서 정규화 된 중심 모멘트는 중심 모멘트를 객체 영역의 거듭제곱한 정규화 계수로 나눈 결과와 같다고 말하고 있다. 고차원 모멘트에서 이 거듭제곱은 더욱 커진다.
중심 모멘트 계산시 moment() 함수에 의해 자동으로 계산되므로 OpenCV에서 정규화 된 모멘트를 따로 계산하는 함수는 없다.
Hu의 불변 모멘트
Hu 불변 모멘트는 1962년에 Hu가 정의한 최대 3차의 정규화 된 공간 모멘트 조합이다. 이러한 불변 모멘트는 이미지의 이동, 회전 및 배율 조정시 변하지 않는다. 따라서 광학 문자 판독(OCR)과 같은 패턴 인식 분야에서 불변 모멘트가 매우 유용하게 사용된다.
Hu 모멘트의 정의는 다음과 같다.
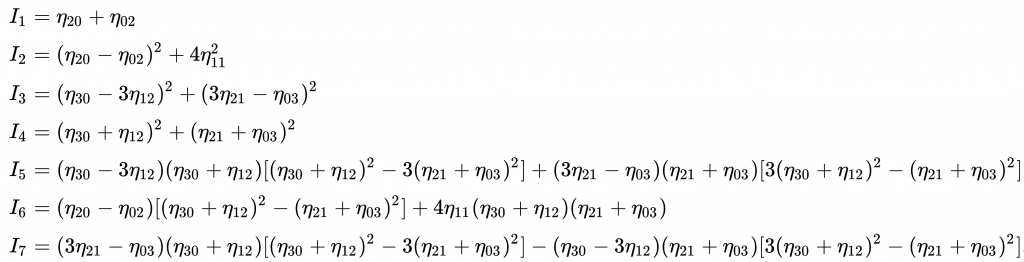
다른 모멘트들은 모두 moments() 함수로 계산 되지만, Hu 불변 모멘트는 moments() 함수로 얻은 배열을 인자로 갖는 HuMoments()함수로 구할 수 있다.
다음 5개의 간단한 문자이미지와 Hu 모멘트를 보면서 원리에 대한 직관력을 얻도록 하자.

| I1 | I2 | I3 | I4 | I5 | I6 | I7 | |
| A | 2.837e-1 | 1.961e–3 | 1.484e–2 | 2.265e-4 | -4.152e-7 | 1.003e-5 | -7.941e-9 |
| I | 4.578e-1 | 1.820e-1 | 0 | 0 | 0 | 0 | 0 |
| O | 3.791e-1 | 2.623e-4 | 4.501e-7 | 5.858e-7 | 1.529e-13 | 7.775e-9 | -2.591e-13 |
| M | 2.465e-1 | 4.775e–4 | 7.263e-5 | 2.617e-6 | -3.607e-11 | -5.718e-8 | -7.218e-24 |
| F | 3.186e-1 | 2.914e-2 | 9.397e-3 | 8.221e-4 | 3.872e-8 | 2.019e-5 | 2.285e-6 |
여기서 흥미로운 사실 한가지는 180도 회전과 반사에서 대칭인 ‘I’가 I3에서 I7에 대해 정확히 0의 값을 갖는다는 것이다. 유사한 대칭을 갖는 ‘O’도 0이 아닌 다른 모멘트를 갖는다.

0개의 댓글