컴퓨터를 이용하여 수학적으로 평면상에 무언가를 그리고 싶을 때, 반드시 알아야 하는 몇가지 재미없는 내용을 정리했다.
원(Circle)
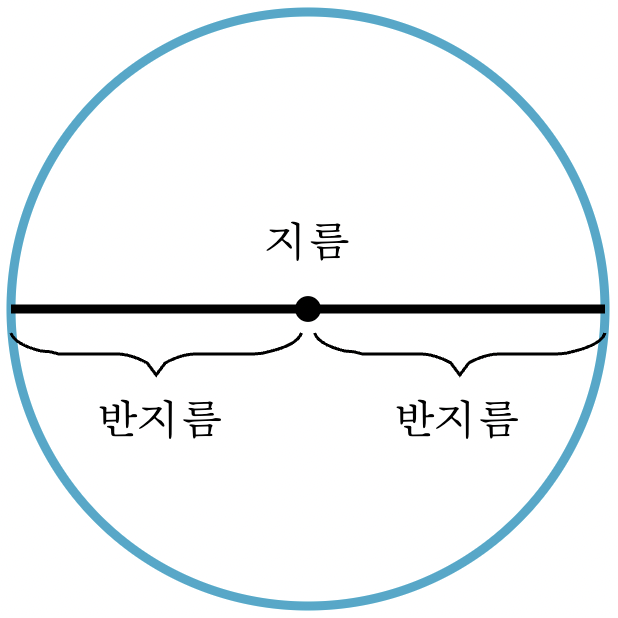
- 지름(diameter) : 원의 중심을 지나 그 둘레위의 두 점을 직선으로 이은 선분의 길이. 한자어로는 직경이라고 하며, 지름은 순우리말.
- 반지름(radius) : 원의 중심에서 그 둘레에 이르는 선분의 길이. 지름의 절반이다.

- 원주(Circumference) : 원의 둘레
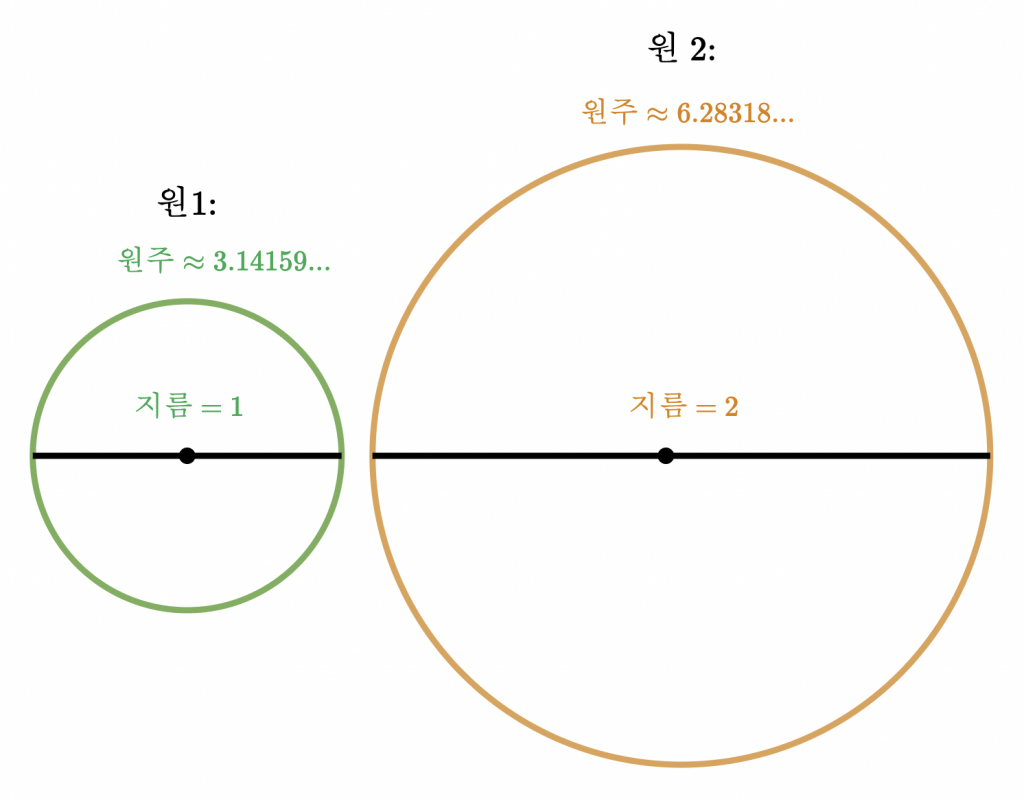
- 원주율(π, pi) : 원의 원주의 지름의 비, 3.141592…
위의 내용을 정리하면 다음과 같은 공식을 유도 할 수 있다.
- 원주 = 원주율 * 지름

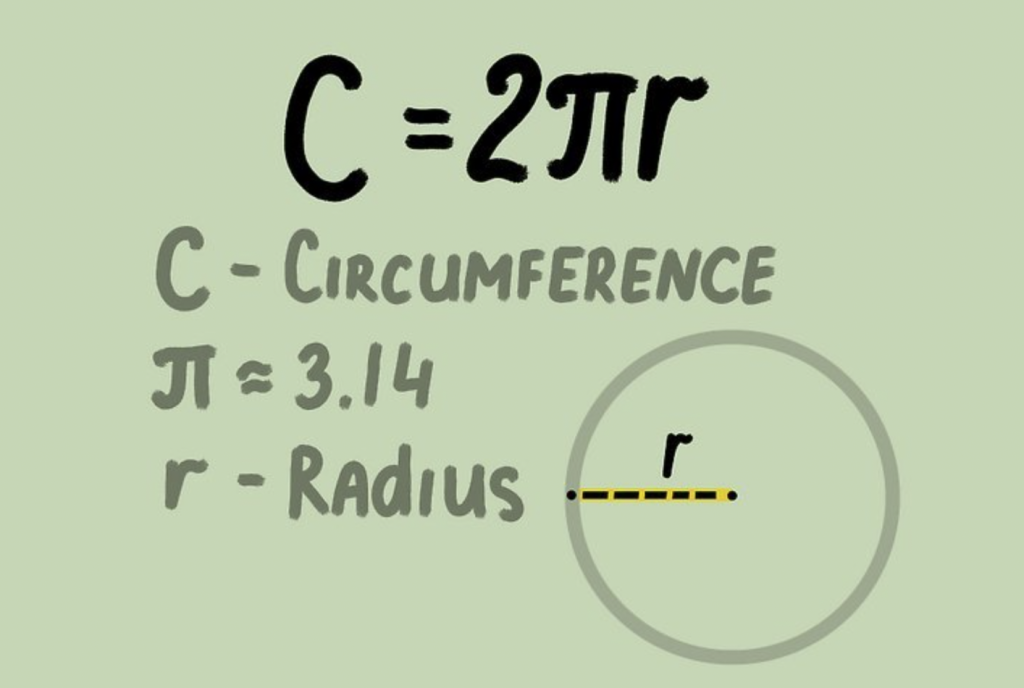
- 원주 = 2 * 원주율 * 반지름
각도(degree)
우리가 친숙하게 사용하는 각(angle)의 단위는 degree(°)이다. degree란 원 한바퀴를 360도로 나누어 표현하는 방법이다. 반원은 180도, 직각은 90도, 피자 한조각은 마시쪙 45도 등 우리에게 매우 익숙한 각의 단위다.
호도(Radian)
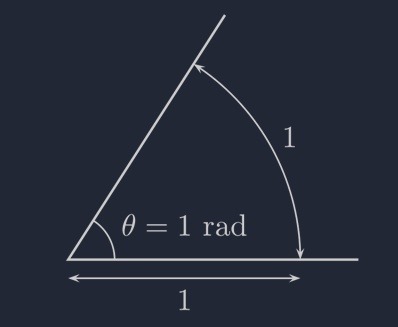
원의 호(arc)는 원주의 일부분을 말하는데, 위의 그림과 같이 호의 길이가 반지름과 같게 되는 만큼의 각을 1 radian(라디안, 호도) 이라고 한다. (1 radian = 약 57.29577951308232°)
위의 그림과 같이 피자 조각 같은 원의 일부를 부채꼴이라고 하는데, 부채꼴 도형에서 반지름, 중심각, 호의 길이는 다음과 같은 관계를 정의 할 수 있다.
중심각(angle) = 호의 길이(arc length) / 원의 반지름 (radius)
즉 3가지 요소 중 2가지를 알면 나머지 하나를 구할 수 있게 된다.
중심각은 흔히 세타(θ)라는 기호를 쓴다. 세타는 각(angle)의 크기를 의미하며 이때 각도(degree)나 호도(radian)를 통해 표현한다.
삼각함수(Trigonometry functions)
삼각함수는 직각삼각형에서 직각이 아닌 한 내각과 나머지 변들에 대한 관계를 정리한 것이다.
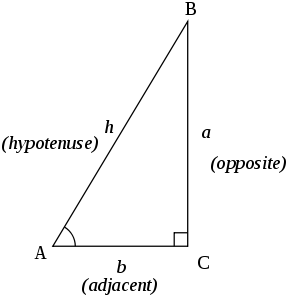
삼각형은 빗변(hypotenuse), 높이(opposite), 밑변(adjacent)로 구성된다. 중심각 A를 기준으로 다음과 같이 삼각함수를 정리할 수 있다.
- cos θ = 빗변 / 밑변
- sin θ = 빗변 / 높이
- tan θ = 밑변 / 높이
이제 삼각함수를 활용하는 예제를 살펴보자
원 그리기
원을 그릴 때는 일반적으로 베지어 곡선을 활용하여 원의 둘레에 해당하는 연속된 점들을 이어 붙이는 방법을 사용하지만, 삼각함수와 원그리기에 대한 이해를 돕기 위해 단순히 원의 둘레에 해당하는 좌표에 점을 찍어 그리는 방법으로 진행해보고자 한다.
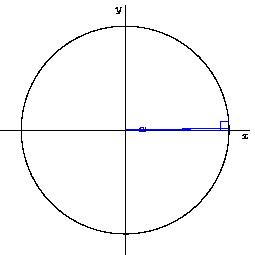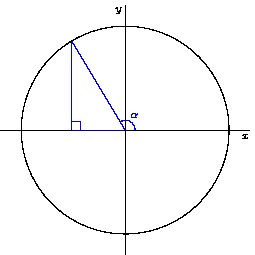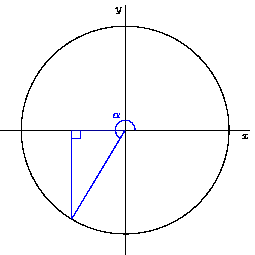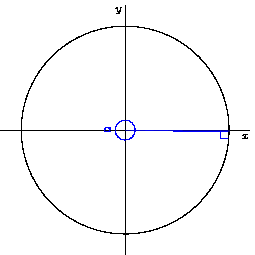
위의 그림을 참고하여 삼각함수를 활용하여 원을 그리자. 그리고자 하는 원에 내접하는 삼각형의 빗변의 길이를 고정한 채로 중심각만 변경하며 원을 그릴 수 있다.
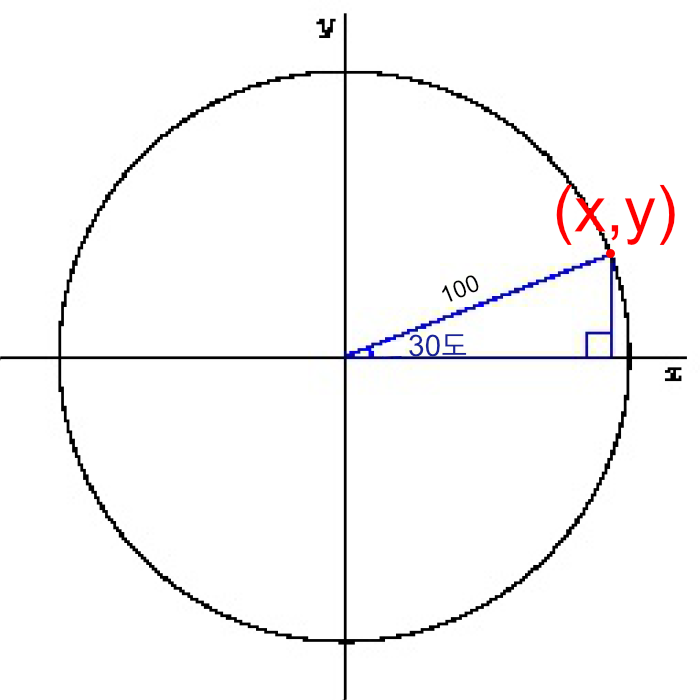
각도를 1도씩 변경하며 점을 360개 찍어볼 것인데, 그 중 중심각이 45도 일 때를 예시로 들어보자. 원의 반지름은 임의로 100으로 설정했다. 이제 원의 둘레에 해당하는 어느 한점인 (x,y)의 좌표를 구해야하는데 삼각함수를 이용하면 간단히 구할 수 있다.
cos을 활용하여 x값을 구해보자.
cos(30도) = 100 / x
√3/2 = 100 / x
x = 200 / √3
y값은 sin을 활용하여 구할 수 있다.
sin(30도) = 100 / y
1/2 = 100 / y
y = 50
중심각이 30도 일 때 (x, y) 는 (200 / √3, 50) 이 된다. 이런식으로 중심각을 1도씩 변경하면서 360개의 점을 찍으면 원을 만들 수 있다.
Compose 의 Canvas를 API를 활용해 위의 예제를 코드로 작성해보자.
/**
* @author soohwan.ok
*/
@Composable
fun Circle(
modifier :Modifier = Modifier,
color:Color = Color.Red,
radius: Float,
width:Float = 1f,
) {
Canvas(modifier = modifier) {
// 각도를 1도씩 변경하면서 점을 찍기 위해 360번 반복
repeat(360) {
// Math API에서는 주로 호도(radian)를 파라미터로 요구하므로 각도를 호도로 변경한다.
val angle = Math.toRadians(it.toDouble())
drawCircle(
color = color,
radius = width,
center = Offset(
x = center.x + cos(angle).toFloat() * radius,
y = center.y + sin(angle).toFloat() * radius
)
)
}
}
}
// 스크린 가로 길이 300으로 고정
private const val width = 300
@Preview(widthDp = width, heightDp = 720)
@Composable
private fun CirclePreview() {
val widthDp = width.dp
var radius by remember { mutableStateOf(100f) }
Column() {
Slider(
value = radius,
onValueChange = {
radius = it
},
valueRange = 0f..widthDp.toPx()/2f
)
Circle(
modifier = Modifier.size(
width = widthDp,
height = widthDp
),
radius = radius,
)
}
}원이 작을 때는 점들로 이루어지는 선이 자연스럽게 이어진 것 처럼 보인다. 하지만 360개의 점으로만 구성하고 있기 때문에 원이 커질 때 선이아니라 점들로 이루어져 있다는 사실을 알 수 있다. 원래 원을 이런식으로 그리진 않는다 이해를 돕기위한 예제일뿐이며, 캔버스에서 원을 그릴때는 drawCircle 함수를 사용하자.
결론
원을 그리는 방법에 대해서 알아보았다. 내용이 길어보이지만 중학교 수학수준의 내용이다. 아마도 다들 이해하셨으리라 생각된다. 원은 다들 그릴줄 알게 되었으니 이제 정오각형은 어떻게 그릴지 한번 상상해보자. 원의 둘레에다가 72도 간격으로 5개의 점을 찍으면 된다. 그것이 바로 정오각형이니까


0개의 댓글