캔버스 기초

이 포스팅은 캔버스의 전반적인 기초에 대해서 요약합니다.

캔버스 좌표계

안드로이드의 캔버스는 다른 좌표계들과 달리 좌측 상단을 원점으로 하여 값이 우측 하단 방향으로 증가합니다.

사각형 그려보기

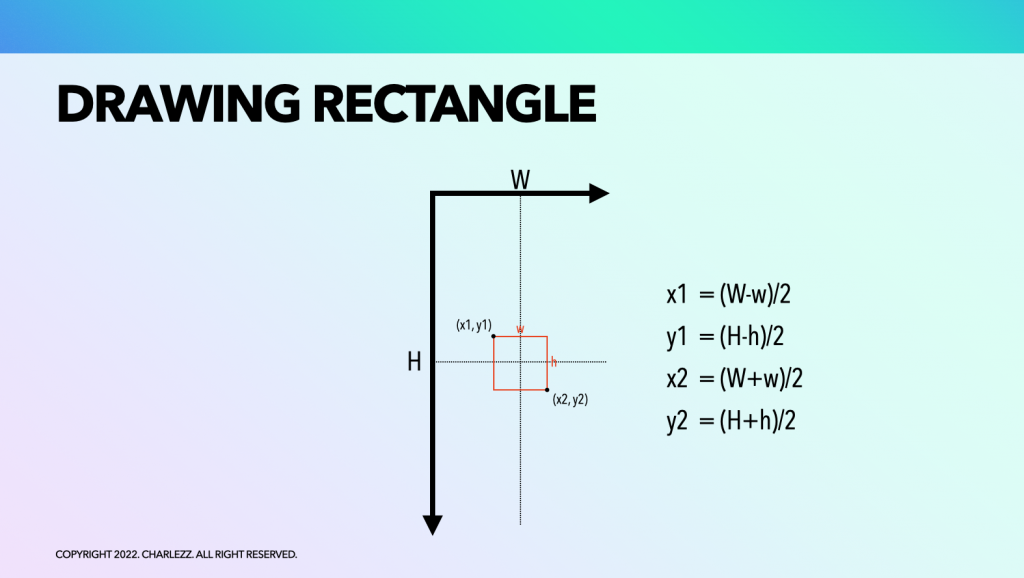
이 캔버스의 정중앙에 사각형을 하나 그리기 위해서는 두 점이 필요합니다. 두 점은 각각 (x1,y1), (x2,y2)로 표현할 수 있습니다. 두 점 대신 하나의 점(x1,y1)과 함께 사각형의 너비, 높이 정보만 있어도 다른 한 점(x2,y2)을 구할 수 있습니다.

정점(x1, y1)에 대한 좌표는 다음과 같은 방정식으로 구할 수 있습니다. 

• x1: (캔버스 너비 – 사각형 너비)/2
• y2: (캔버스 높이 – 사각형 높이)/2로

비슷한 방법으로 두번째 정점도 구합니다. 그런 뒤 사각형 그리기 API(예: drawRect)를 호출하여 사각형을 그립니다.

그리기 API

도형을 그릴 때 자주 사용할만한 drawing API들 입니다. (예제코드)

위에서 부터 사각형, 원, 선, 타원, 호, 둥근 사각형을 그립니다.

브러쉬 종류

기본적으로 제공하는 브러쉬의 타입은 다음과 같습니다.

• 선형(Linear)
• 방사형(Radial)
• 가로형(Horizontal)
• 세로형(Vertical)
• 스윕형(Sweep)

그리기 스타일

DrawStyle에는 두가지 타입이 있습니다.

• Fill : 도형의 면을 채움
• Stroke : 도형의 선만 그림

선(Stroke) 스타일

Stroke는 다음과 같은 부가적인 스타일 속성을 갖습니다.

• width
• miter
• cap
• join
• PathEffect

Stroke의 width는 선의 두께를 표현합니다.

Cap과 Join은 위 그림으로 하나로 설명할 수 있습니다.

Cap은 선끝의 마감을 어떤식으로 처리할 지를 결정합니다.

• Butt : 선의 끝지점에서 반듯이 잘라서 마감처리
• Square : 선의 끝지점을 중점으로 하여 정사각형으로 마감처리
• Round : 선의 끝지점을 중점으로 하여 정원을 그려, 둥글게 마감처리

Join은 선분 사이의 결합되는 관절 부분으로 이 부분을 어떻게 표현할 지 결정합니다.

• Round : 둥글게 마감처리
• Bevel : 선분의 맞닿는 끝 모서리를 연결하여 비스듬한 모양 제공
• Miter : 선분사이의 결합부분에 날카로운 모서리를 형성

Miter의 경우 모서리의 길이를 다음 그림과 같이 제한할 수도 있습니다.

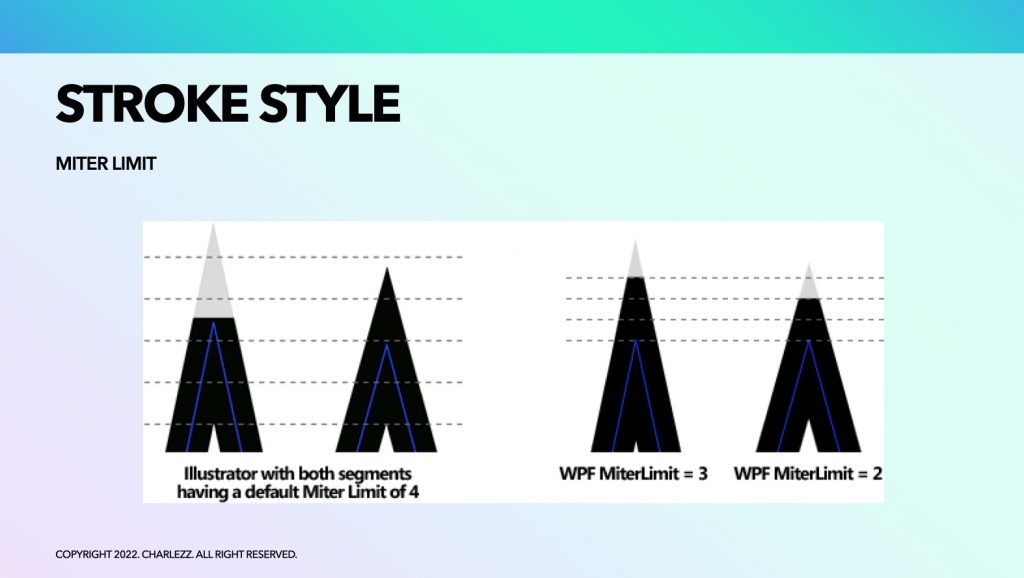
두 선분 사이에서 join 스타일이 miter로 결합된 경우 날카로운 부분의 경계를 지정할 수 있습니다.

변형(Transformation)

변형은 캔버스에 그리고자 하는 내용을 이동(translate), 확대(scale), 회전(rotate) 할 때 씁니다.

변형 예제코드

이동 예제

미리보기 이미지의 흰 점선 도형은 ‘변형’ 이전의 도형을 의미합니다.

확대 예제

회전 예제

삼각법

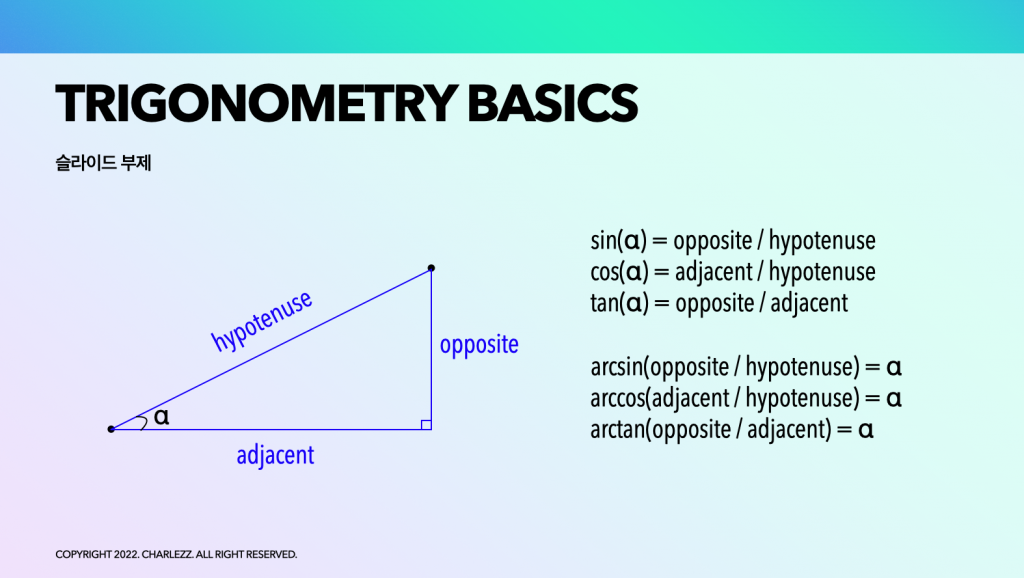
직각 삼각형은 한 각이 직각, 즉 90도인 삼각형을 말합니다. 이 때 다른 각도 알파(α)를 구하는 방법과 그와 관련된 내용에 대한 이야기를 해보겠습니다.

먼저 이 삼각형의 빗변(hypotenuse), 밑변(adjacent), 높이(opposite)를 삼각함수(α)로 나타내면 다음과 같습니다.

• sin(α) = 높이 / 빗변
• cos(α) = 밑변 / 빗변
• tan(α) = 높이 / 밑변

역삼각함수를 구하면 알파값(a)을 구할 수 있게 됩니다.

• α = arcsin(높이 / 빗변)
• α = arccos(밑변 / 빗변)
• α = arctan(높이 / 밑변)

계산같은 복잡한 내용은 필요없습니다. 우리는 알파값(α)을 구하는 과정에만 집중하면 됩니다. 우리가 사용하는 프로그래밍 언어(자바와 코틀린)에서는 삼각함수에 관련된 함수들을 이미 제공하고 있습니다.

자 그럼 이제 실전연습을 해볼까요. 삼각형 내의 직각을 제외한 한 각 알파(α)를 구해봅시다.

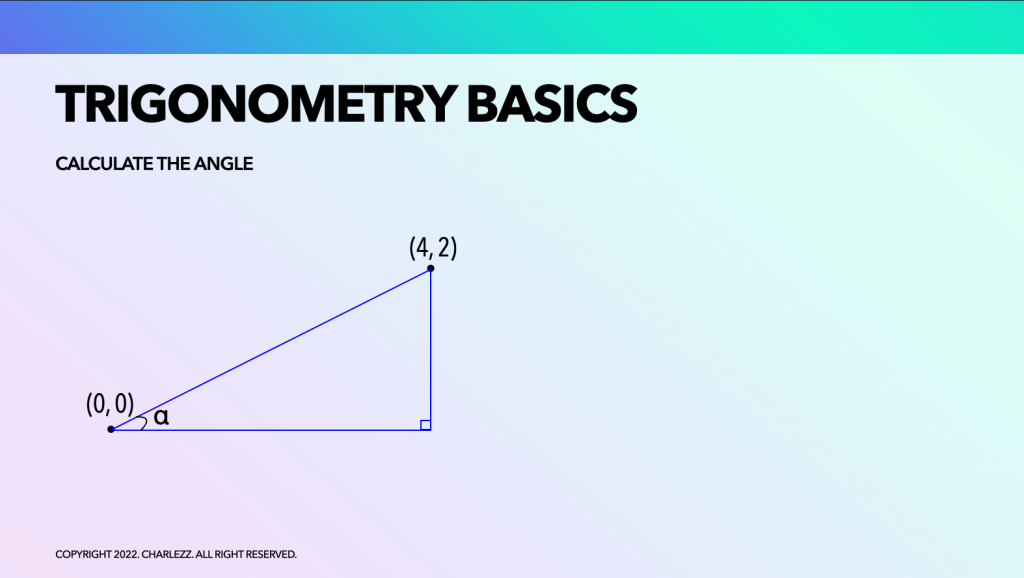
위와 같은 직각 삼각형이 주어졌고, 빗변과 연관된 두 정점의 좌표를 알고 있습니다. 그렇다면 이 직각삼각형의 밑변의 길이는 4이고, 높이는 2라는 것을 직관적으로 알 수 있습니다. 밑변과 높이를 알면 아크 탄젠트 함수를 사용하여 알파를 구할 수 있습니다.

알파는 0.46 radian이며, 이 값은 약 26.5도에 해당합니다.

각도(degree)와 호도(radian)

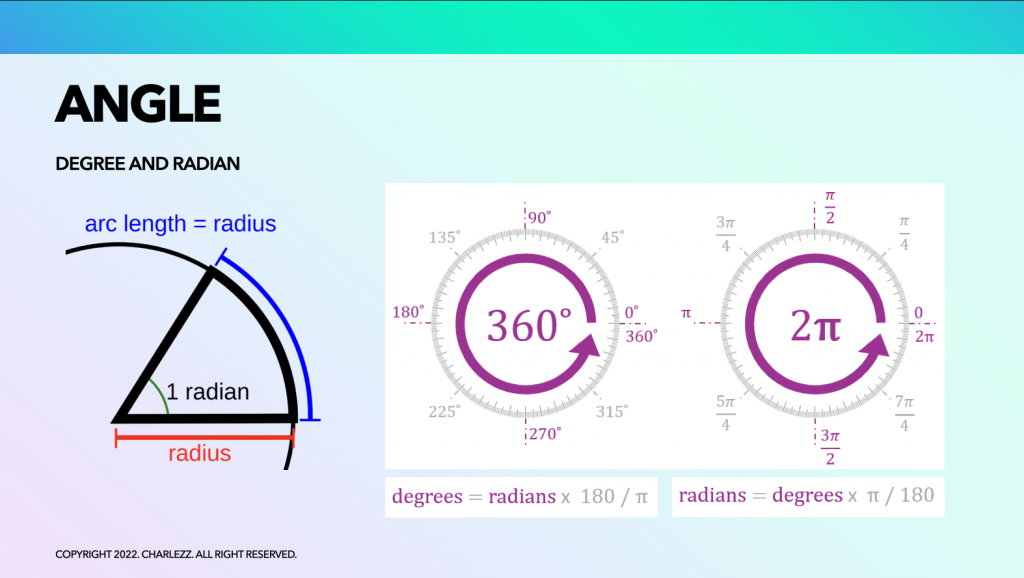
각(angle)과 각도(degree)는 다릅니다.

한 점으로 부터 두 방향으로 나간 두개의 반직선이 벌어진 정도를 각이라고 합니다. 이 각을 표현하는 방법은 두가지가 있습니다. 그것이 바로 각도와 호도입니다. 

• 각도 : 원을 360도로 나누어 표현
• 호도 : 원의 반지름과 호가 같을 때의 각을 1 radian으로 정의하여 표현

컴퓨터 분야에서는 보통 radian 방식으로 표현합니다.

극좌표계

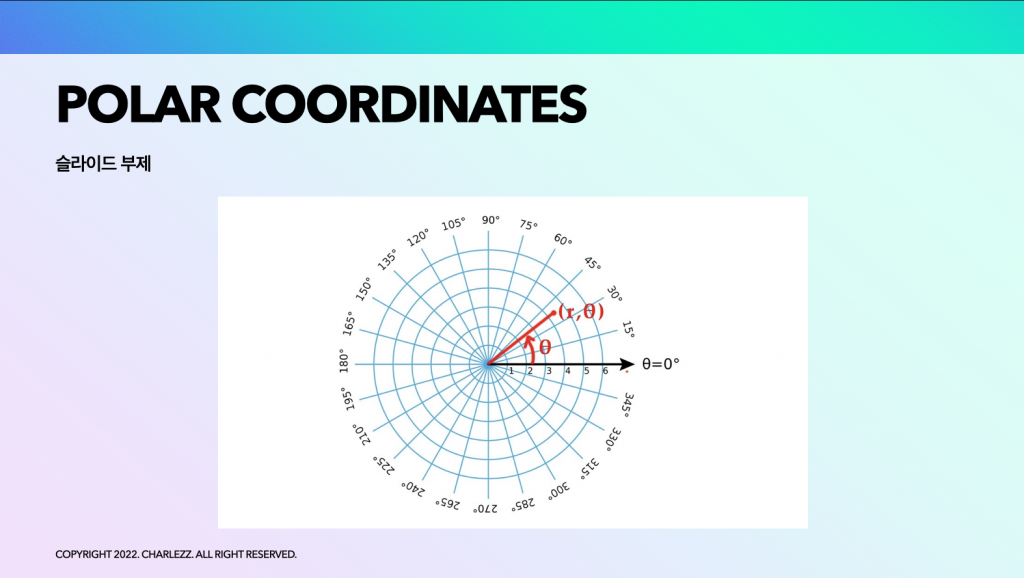
극좌표계는 평면 위의 위치를 각도와 거리를 써서 나타내는 2차원 좌표계입니다. 안드로이드 캔버스와 같은 직교 좌표계에서 복잡하게 표현되는 수식이, 극좌표계에서는 간단하게 표현되기때문에 많이 사용합니다.

극좌표계를 사용하는 다음 예제를 살펴보겠습니다.

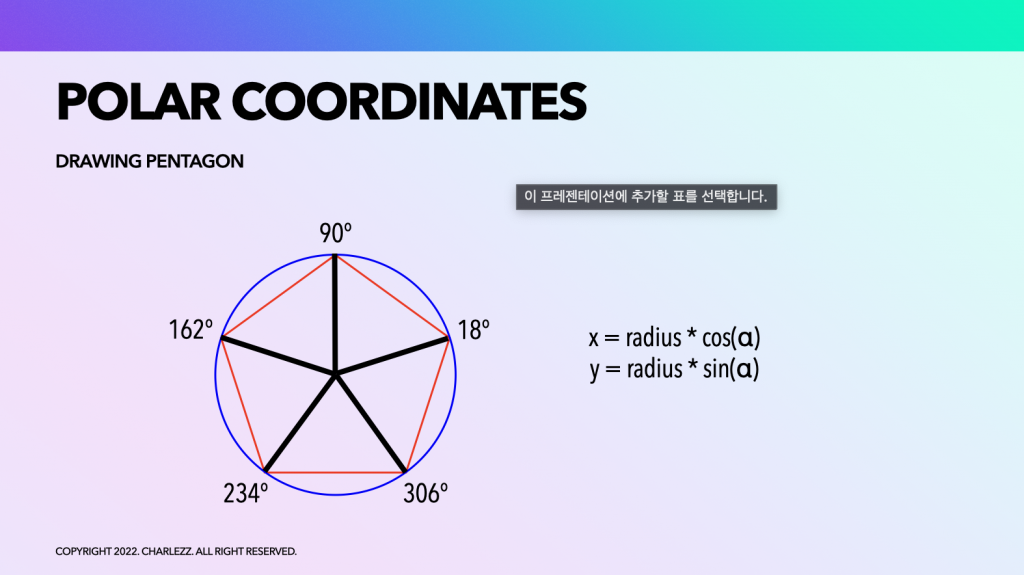
정오각형을 극좌표계에서는 쉽게 그릴 수 있습니다.

오각형이니, 360도를 기준으로 나누기 5를 하여 초기 각도로부터 72도씩 늘려가며 원의 반지름에 해당하는 지점에 정점을 찍고 각 정점들을 이어주면 수학적으로 완벽한 정오각형을 만들 수 있습니다.

클릭 영역 판별

빨간색에 해당하는 부분만 클릭되게 어떻게 해야할까요? 좀 더 크게 확대해서 살펴보겠습니다.

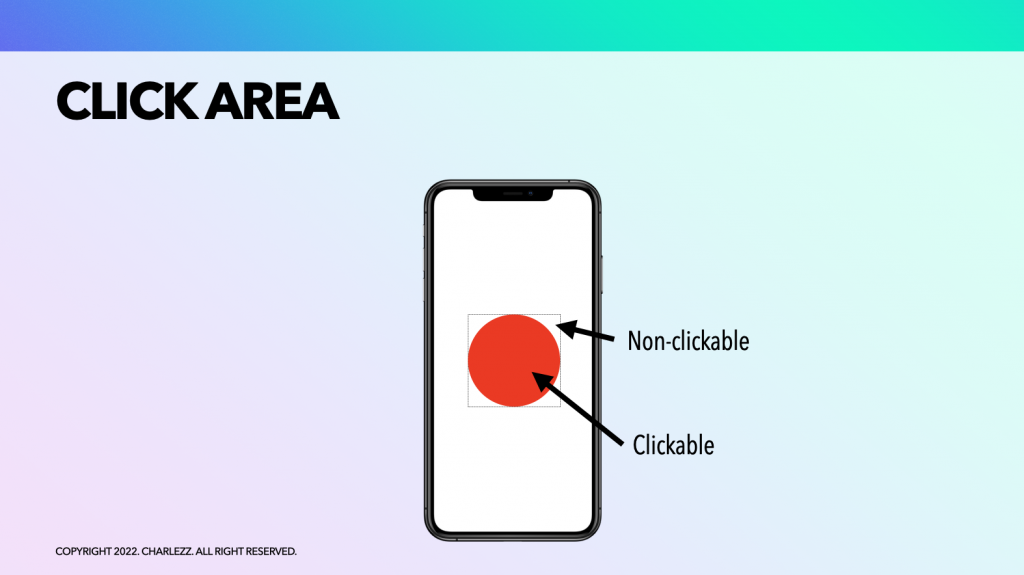
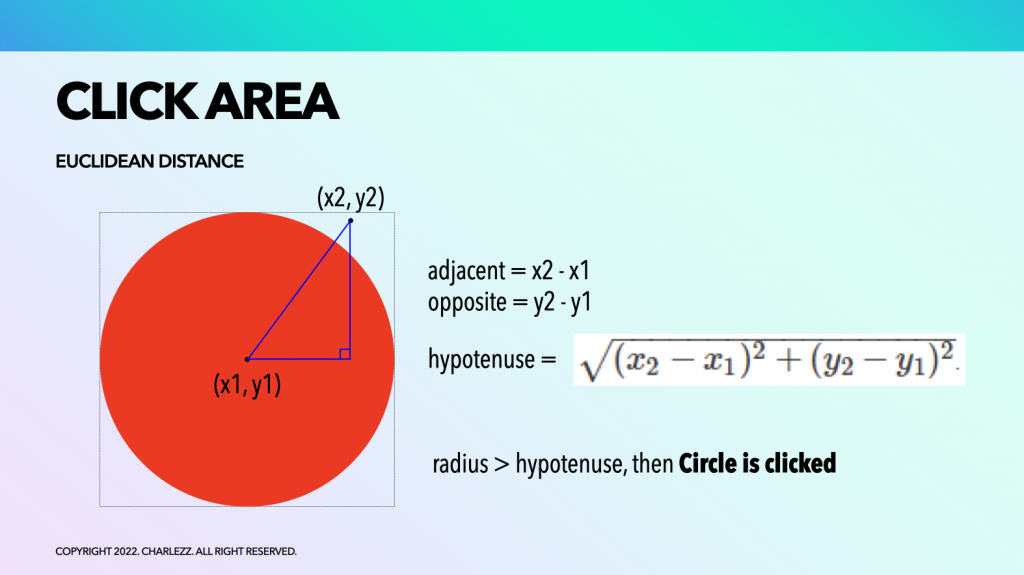
원의 중점과 사용자가 클릭한 영역인 임의의 정점이 있다고 가정해봅니다.

두 점을 이어 빗변을 갖는 직각삼각형을 얹어 보겠습니다. (이제 아마 감이 오실 듯..)

피타고라스 정리에 따르면 빗변의 길이는 다음과 같은 방정식으로 구할 수 있습니다.

• 빗변 = sqrt( (밑변)^2 + (높이)^2 )

즉 원의 반지름이 이 삼각형의 빗변보다 크다면 클릭으로 판정할 수 있습니다.