매트릭스의 세계로…
지금까지는 점 , 선, 삼각형 또는 삼각형 결합을 통한 다각형을 그리는 방법에 대해서 알아보았습니다.
하지만 이는 평면상의 2D그래픽이지 3D는 아니였습니다. 또한 정사각형이 나오길 기대했으나 직사각형으로 나타나는 것을 볼 수 있었습니다. 사실 코드로 정사각형으로 표현하는 방법은 매우 간단하지만, 이해하기는 쉽지가 않기 때문에 이전 포스트에서는 다루지 않았습니다. 그래서 이번장에는 미루고 미뤄왔던 매트릭스에 대해서 알아보고자 합니다.
매트릭스란(행렬)?
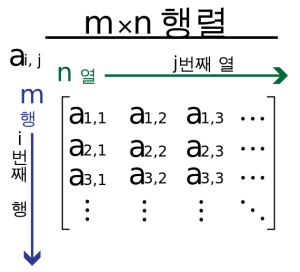
수학에서 수나 기호, 수식 등을 네모꼴로 배열한 것입니다.
행렬은 물리학에서 전기회로, 양자 역학 등에서 쓰이고, 컴퓨터 그래픽스에서 3차원 이미지를 2차원 평면에 투영하거나 사실적인 움직임을 그려내기 위해서 사용합니다.
OpenGL에서의 매트릭스
| A00 | A01 | A02 | A03 |
| A04 | A05 | A06 | A07 |
| A08 | A09 | A10 | A11 |
| A12 | A13 | A14 | A15 |
표1. 사람이 일반적으로 이해하는 4 x 4 , 2차원행렬의 모습
OpenGL을 사용하는 3D 그래픽스에서는 위의 표1과 같이 4 x 4 정방행렬을 주로 사용하게 됩니다.
위와 같은 행렬을 열우선 배치로 컴퓨터 메모리상에 배치하면 다음과 같은 형태를 띄게 됩니다.
float[] A = new float[16];
표2. 컴퓨터의 메모리 상의 1차원 행렬
OpenGL을 다루는 개발자에게는 표2의 형태가 친화적입니다.
행렬과 벡터는 3D그래픽스 프로그래밍에서 자주 보게될 친구들입니다. 이러한 용어를 사용할 때 스칼라라는 용어도 함께 사용되는데, 스칼라는 크기 또는 특정 양을 나타낼 때 사용합니다. 즉, 벡터에서 방향성을 제거한 녀석입니다. 예를들면, 속력은 스칼라이고, 속도는 벡터입니다.
매트릭스는 매트릭스끼리 연산할수도 있지만, 벡터나 스칼라값과도 곱할 수 있습니다. 이게 아직은 무슨 의미인지 와닿지 않을 것입니다. 우리는 한점의 위치나 도형을 나타내기 위해 정점(벡터로 나타낸)을 사용해왔습니다. 이 값을 매트릭스에 곱해 변환된 새로운 정점(다른 벡터)을 만들 수 있다는 의미입니다.
수식으로 살펴보자면 아래와 같습니다.
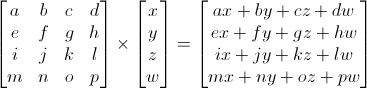
매트릭스와 벡터의 곱을 통해 새로운 벡터를 얻었습니다!
걱정마세요 직접 계산할 일은 없을겁니다.
| Note : 행렬 x 정점 = 변현된 정점 반드시 이 순서로 곱해야 합니다. 매우 중요합니다. |
Identity Matrix(단위행렬)
단위행렬은 임의의 벡터를 단위행렬에 곱해도 벡터가 변하지 않는 행렬입니다.
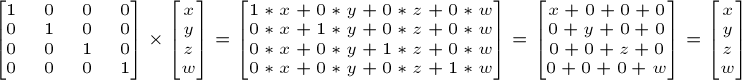
벡터 (x,y,z,w)를 4×4 매트릭스에 곱해도 여전히 벡터 (x,y,z,w)로 남아있는것을 위의 식에서 확인할 수 있습니다.
안드로이드에서는 단위행렬을 다음과 같이 생성할 수 있습니다.
float[] matrix = new float[16]; Matrix.setIdentityM(matrix, 0);
Translation Matrix(평행이동 행렬)
정점 (10,10,10) 이 있다고 가정합시다.
변환 이 정점을 x방향으로 10만큼 평행 이동 시키려면 어떻게 해야할까요?
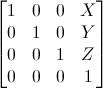
이동에 관련된 행렬은 이렇게 생겼습니다.
단위행렬에서 우측의 X,Y,Z값이 이동하는 성분을 뜻합니다.
정점 (10,10,10)을 x방향으로 10만큼 이동하기로 했으니 한번 해보겠습니다.
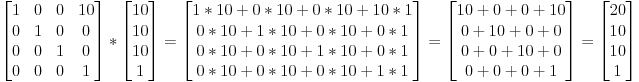
생각보다 간단합니다. (20,10,10,1) 의 동차좌표계의 벡터를 얻었습니다.
w값이 1이니 여전히 동차좌표에서 위치를 뜻하기도 합니다.
그럼 이번엔 정점이 아닌 방향성을 가지는 w값이 0인, (0,0,-1,0)을 x방향으로 10만큼 이동해볼까요?
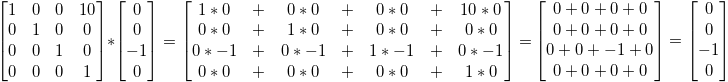
여전히 (0,0,-1,0)입니다. w가 0이니 방향을 나타내고, 벡터가 이동을 하였더라도 크기와 방향이 같으므로 여전히 같은 벡터입니다. 신기합니다.
안드로이드에서는 다음과 같이 평행이동을 위한 행렬을 만듭니다.
float[] matrix = new float[16]; Matrix.setIdentityM(matrix,0); Matrix.translateM(matrix, 0, 10,0,0);
| Note : 실제로 matrix 배열을 확인해보면 성분의 순서가 그림과는 다를 수 있는데, 설명하는 부분에는 열우선(columns-major) 이고, 안드로이드에서는 행우선(rows-major)으로 처리하기 때문입니다. |
Scaling Matrix(확대/축소 행렬)
스케일링 매트릭스의 형태는 이렇습니다.
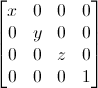
x,y,z에 해당하는 부분에 원하는 값을 넣으면 확대 또는 축소를 시킬수 있습니다.
모든 방향에 대해 2배 확대하고 싶다면,
| 2, 0, 0, 0 0, 2, 0, 0 0, 0, 2, 0 0, 0, 0, 1 |
2배 축소 하고 싶다면.
| 0.5, 0, 0, 0 0, 0.5, 0, 0 0, 0, 0.5, 0 0, 0, 0, 1 |
입니다.
어떠한 벡터에 대해 두 배 확대한 결과입니다.
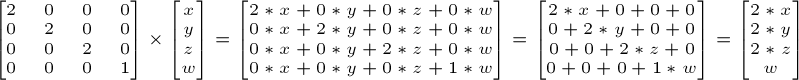
Rotation Matrix(회전 매트릭스)
회전 행렬은 삼각함수를 써야 하므로 스케일링 행렬이나 이동행렬처럼 단순하진 않습니다.
3D그래픽스에서 어떤 오브젝트를 회전하기 위해서는 어떤 한축을 기준으로 몇도만큼 회전 할 것인지를 정해야합니다. 이때의 각도를 쎄타라고 가정하겠습니다.
행렬의 곱셈은 결합 법칙이 성립하므로 위에서 구한 x,y,z의 회전 값을 순서대로 곱하면 됩니다. 이를 오일러각(Euler Angles)라 합니다. 오일러각으로 물체를 회전 할 때는 회전 순서에 주의하여야 합니다.각 x,y,z의 각 축은 서로 종속적이기 때문에 한축이 회전시 다른축에 영향을 미칩니다. 그로인해 회전 순서에 따라 물체의 회전된 최종 방위가 달라집니다. 일반적으로 ZXY(Roll-Pitch-Yaw) 또는 XYZ 회전이 주로 사용됩니다. 이와 같은 특성때문에 짐벌락이라는 현상이 발생합니다.
안드로이드에서 회전 행렬을 만들기 위해서는 다음과 같은 코드를 사용합니다.
Matrix.setRotateM(float[] rm, int rmOffset, float a, float x, float y, float z)
- rm : 매트릭스
- rmOffset : 매트릭스 배열의 시작점, float형 16개짜리 배열을 사용한다면 당연히 0이 된다.
- a : 회전하고자 하는 각도
- x : x축 회전 벡터
- y : y축 회전 벡터
- z : z축 회전 벡터


4개의 댓글
forest104 · 2019년 9월 30일 2:06 오전
좋은 글 감사합니다~
Charlezz · 2019년 9월 30일 4:57 오후
감사합니다 🙂
Chris Lim · 2019년 9월 30일 10:08 오후
감사합니다. 잘 읽었습니다!
Charlezz · 2019년 10월 2일 11:36 오후
감사합니다 🙂